An interesting classification problem is trying to find a decision boundary that separates two categories of points. For instance, consider the following cloud of points:
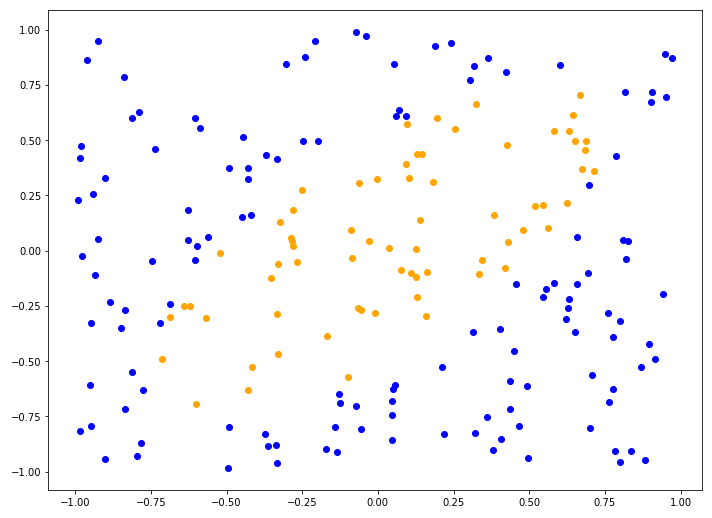
We could hand draw a line that separates the two colors. But can this problem be solved automatically?
Several machine learning methods could be used for this, including for instance a Support Vector Machine or AdaBoost. What all of these methods have in common is that they perform complex calculations under the hood and spill out some number, that is, they are black boxes. An interesting comparison of several of these methods can be found here.
A simpler and more elegant alternative is to try to find an explicit mathematical formula that separates the two categories. Not only would this be easier to compute, but it would also offer some insight into the data. This is where symbolic regression comes in.
Symbolic regression
The way to solve this problem with symbolic regression is to look for a formula that returns 0 for points of one category and 1 for points of another. In other words, a formula for classification = f(x, y).
We can look for that formula by generating a CSV file with our points and loading it into TuringBot. Then we can run the optimization with classification accuracy as the search metric.
If we do that, the program ends up finding a simple formula with an accuracy of 100%:
classification = ceil(-1 * tanh(round(x * y - cos(-2 * (y - x)))))
To visualize the decision boundary associated with this formula, we can generate some random points and keep track of the ones classified as orange. Then we can find the alpha shape that encompasses those points, which will be the decision boundary:
from math import *
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import ConvexHull
def f(x, y):
return ceil(-1 * tanh(round(x * y - cos(-2 * (y - x)))))
# Generate points
pts = []
for _ in range(10000):
x = np.random.random() * 2 - 1
y = np.random.random() * 2 - 1
if f(x, y) == 1:
pts.append([x, y])
pts = np.array(pts)
# Compute the convex hull
hull = ConvexHull(pts)
hull_pts = pts[hull.vertices]
# Plotting
fig, ax = plt.subplots()
ax.plot(pts[:, 0], pts[:, 1], 'o')
for simplex in hull.simplices:
ax.plot(pts[simplex, 0], pts[simplex, 1], 'k-')
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
plt.show()
And this is the result:
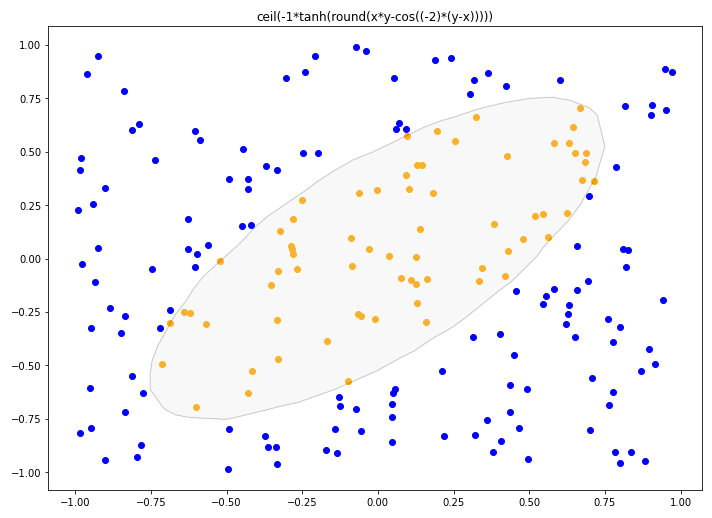
It is worth noting that even though this was a 2D problem, the same procedure could have been carried out for a classification problem in any number of dimensions.