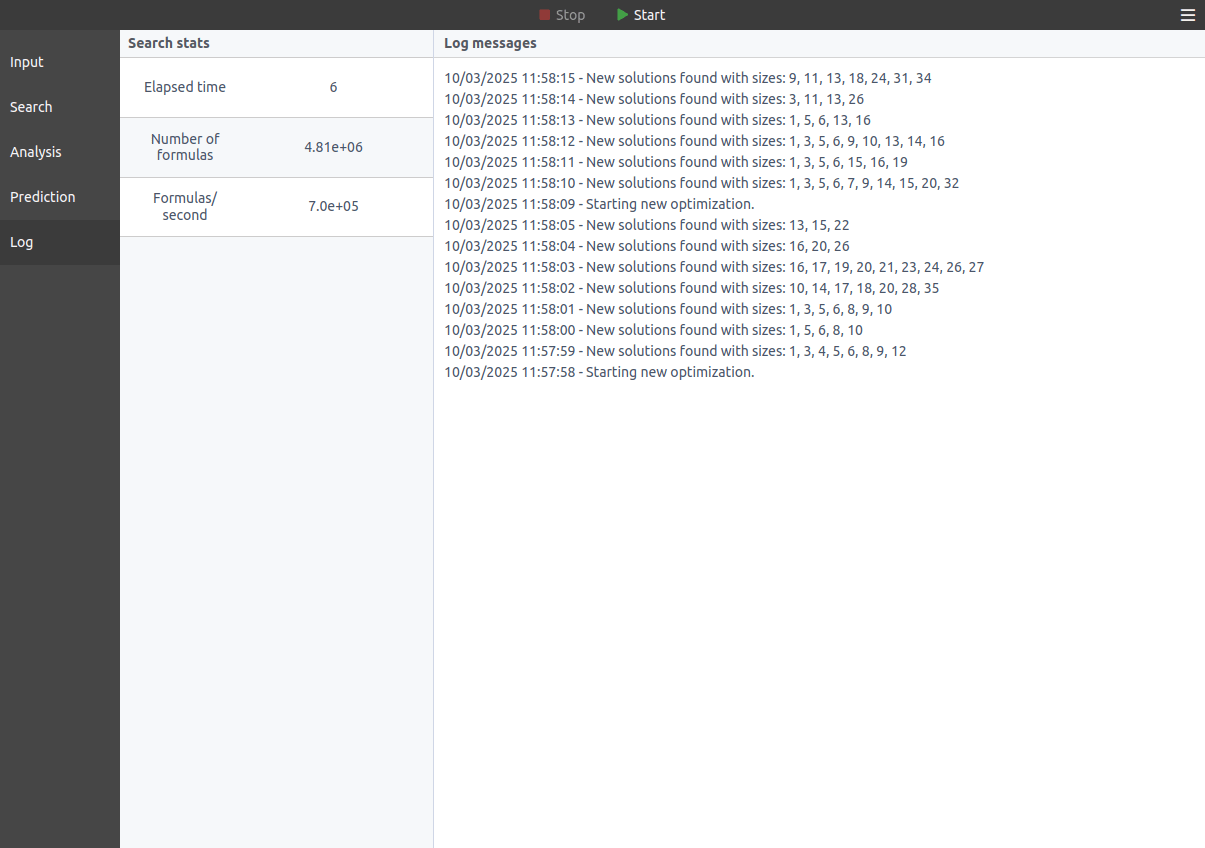
Turn your data into formulas that actually make sense
Predicting numerical values from input variables can be challenging. Simple models like linear or polynomial regression often fail to capture complex patterns, while complex machine learning methods can be difficult to interpret and trust.
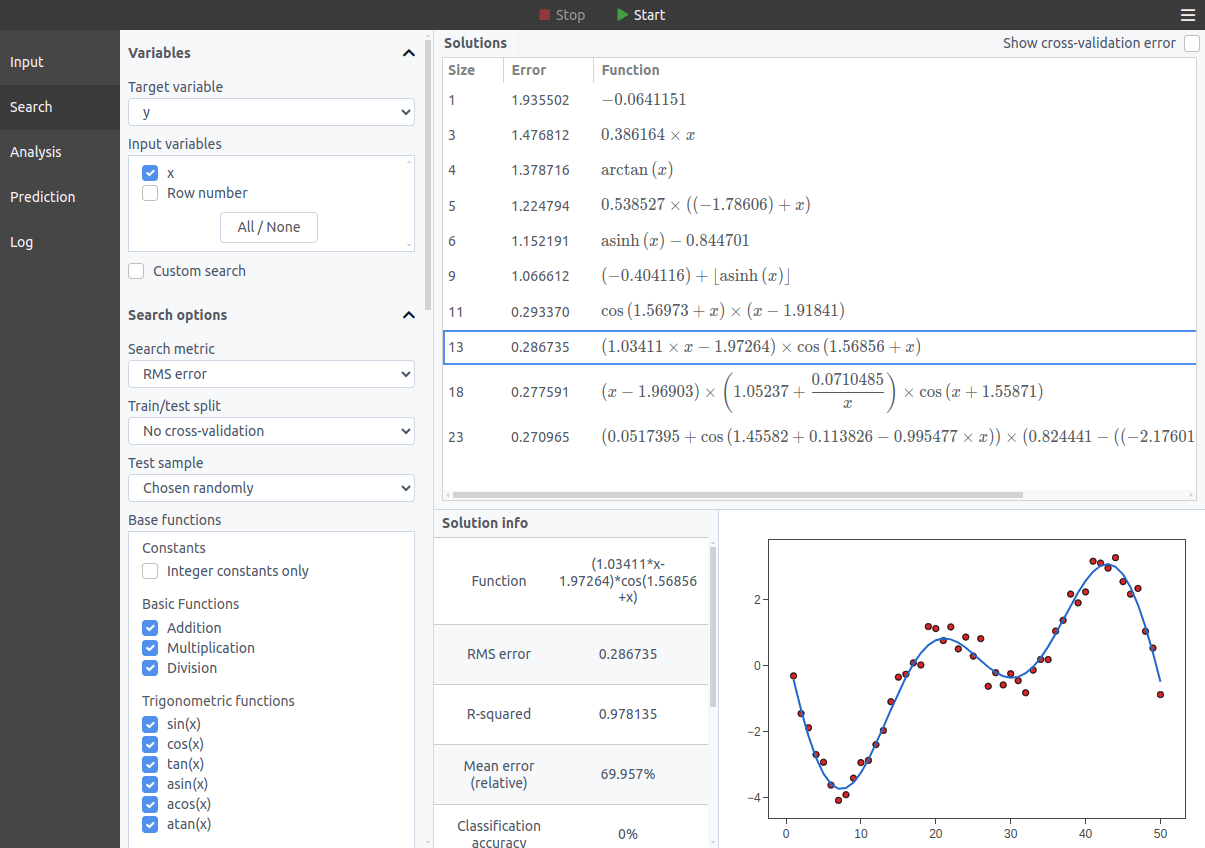
TuringBot uses Symbolic Regression to discover clear mathematical formulas that describe your data. The result: models that are accurate, robust, and explainable.
Given input variables like x and z, it can automatically find a relationship such as y = f(x,z).
How does it work?
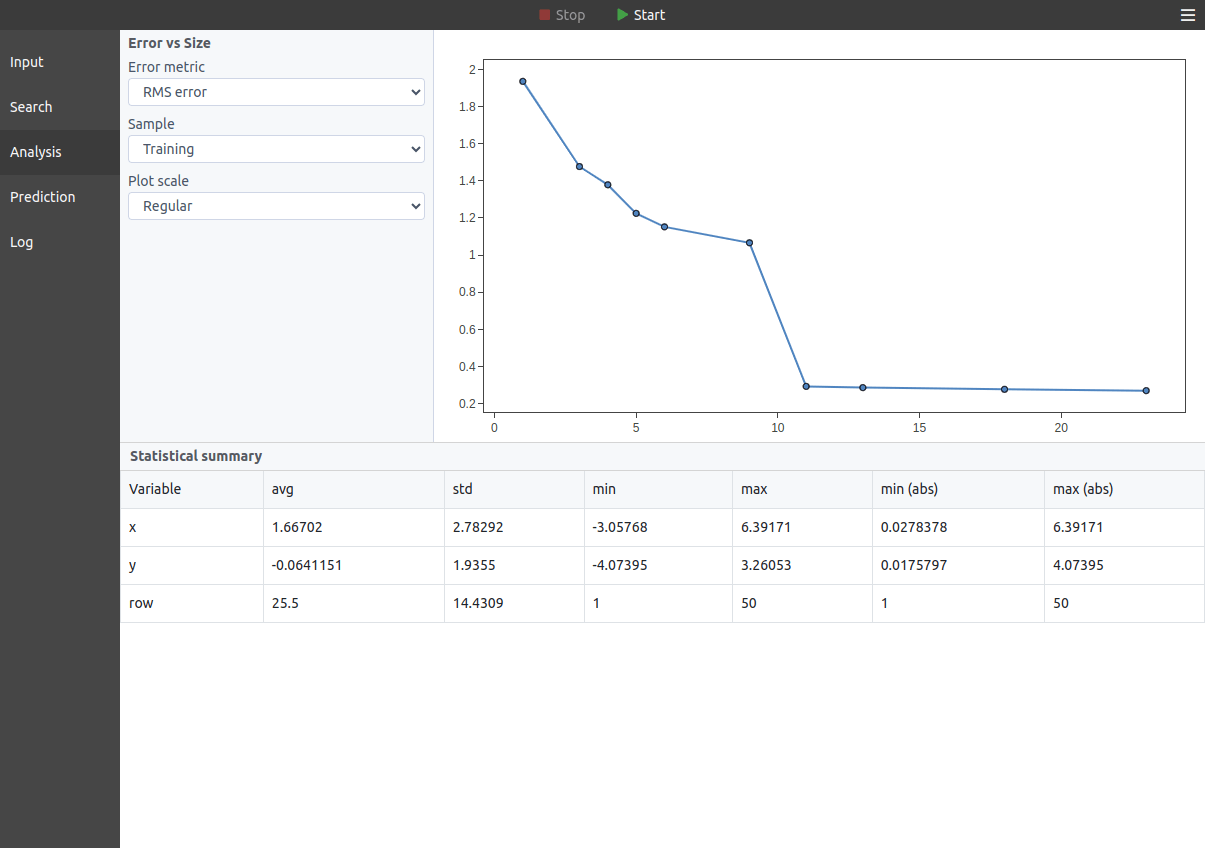
TuringBot implements a technique called Symbolic Regression. It tries to combine a set of base functions into simple formulas that accurately predict a target variable as a function of one or more input variables. The base functions offered by the program are the following:
- Arithmetic: addition, multiplication, division
- Trigonometric: sin, cos, tan, asin, acos, atan
- Exponential: exp, log, log2, log10, sqrt, pow
- Hyperbolic: sinh, cosh, tanh, asinh, acosh, atanh
- Logical: smaller, greater, equal, different, min, max, logical_or, logical_and
- History: delay, moving_average
- Other: abs, floor, ceil, round, sign, fmod, tgamma, lgamma, erf
What is optimized is the formula itself, and not just the numerical constants of some assumed model.
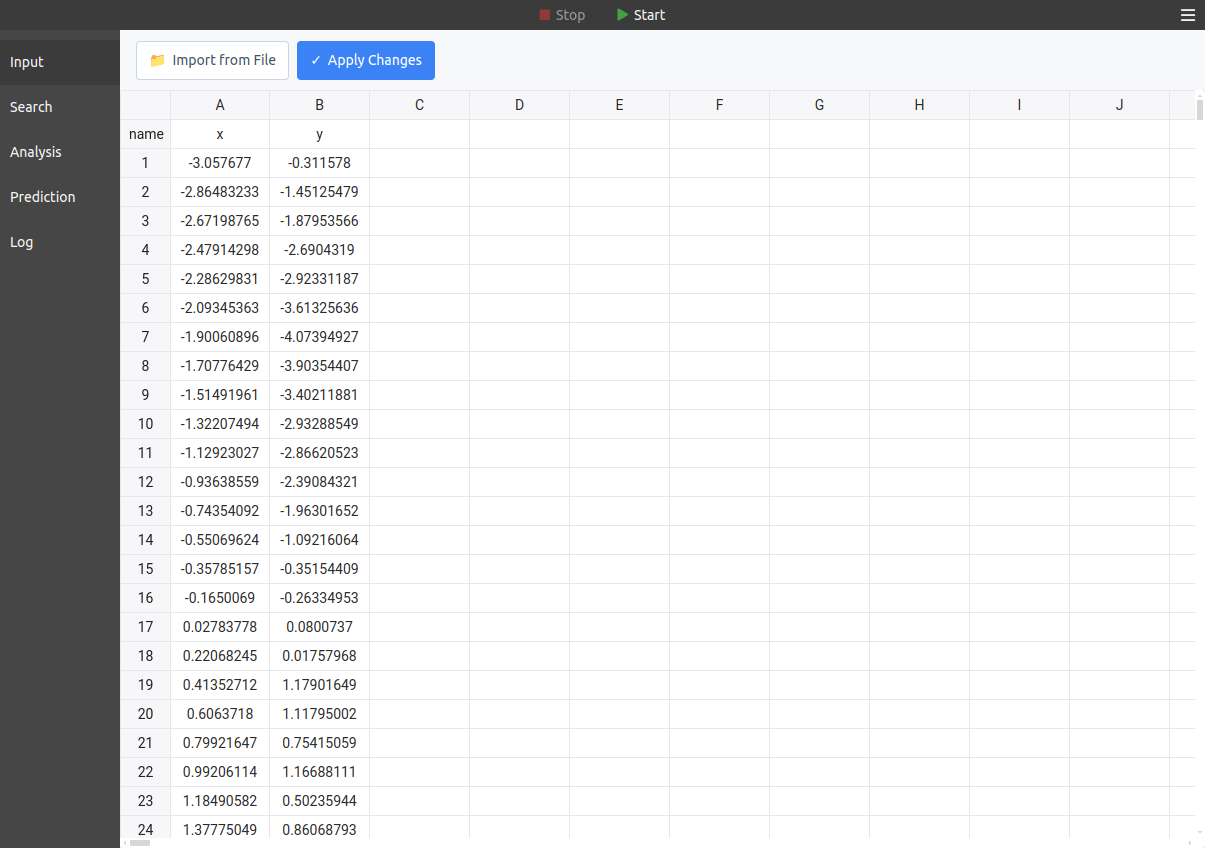
You can paste data directly into the built-in spreadsheet or import TXT and CSV files with any number of columns. The program can be used both interactively through its graphical interface or in an automated way from the command line.
Here is an example of an input file that you can use: input.txt.
Why choose TuringBot?
- Proven track record: TuringBot has been successfully employed in academic publications across a wide range of fields.
- High performance: Written in optimized C++ and powered by a novel search algorithm, TuringBot searches significantly faster than alternatives based on Python or JIT-compiled languages like Julia.
- Customizable search: Define your own base functions, constants, error metrics, and formula templates to tailor the search to your domain. See the documentation for details.
- Easy setup: It is a self-contained executable that you can install in a few minutes. No Python dependencies, no Docker, no Conda, no virtual environments. This makes it easy to get started and focus on your work.
- CLI and Python library: TuringBot includes a full command-line interface and a Python library for integration into scripts, pipelines, or any automated workflow.
- Active development: TuringBot's development began in 2019, and version 1.0 was launched to the public in February 2020. Since then, the program has been continually updated in response to user feedback. See the changelog for details.
What can TuringBot be used for?
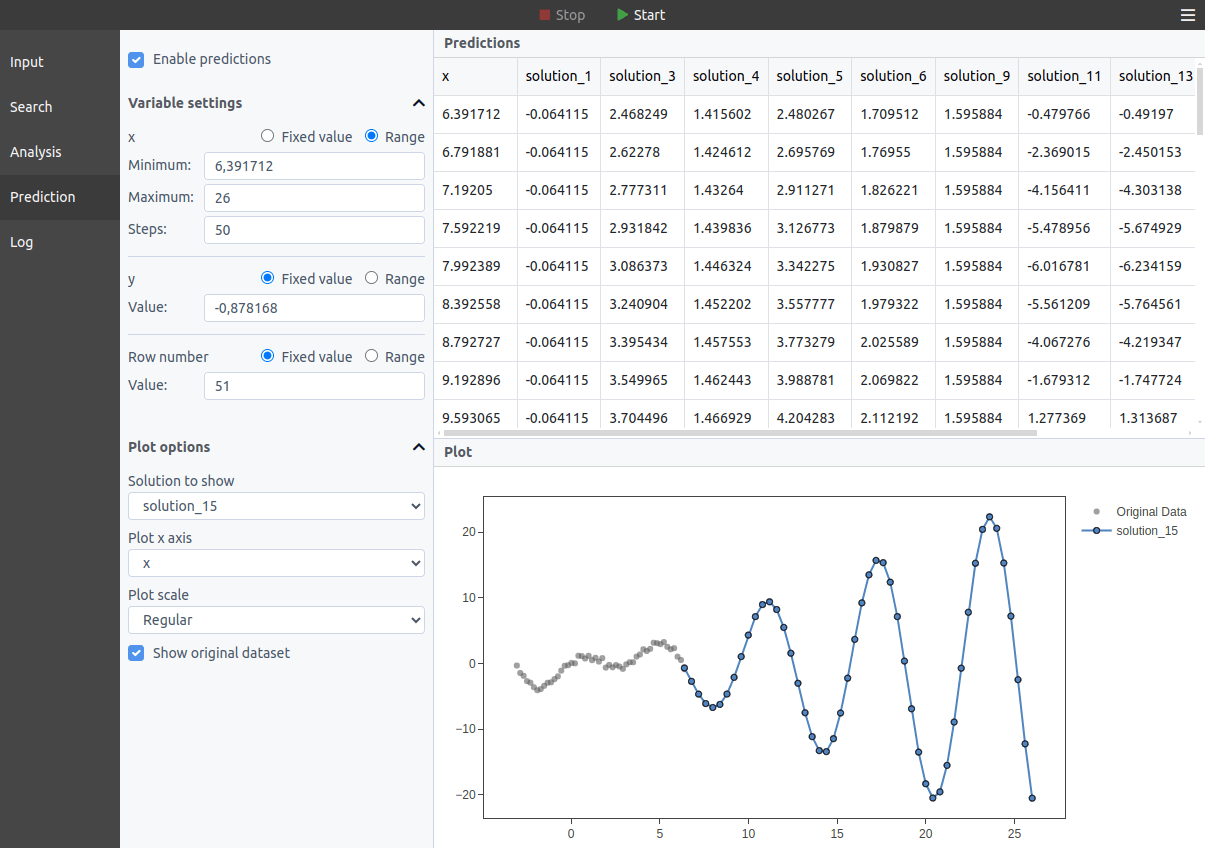
If your problem involves predicting a number as a function of other numbers, then you can apply TuringBot to it. Just paste your data into the built-in spreadsheet or import a TXT/CSV file, and start the search.
To give a few concrete examples:
- Predict the price of a house as a function of its characteristics (area, number of bedrooms, age, etc): A regression model example and how to generate it.
- Detect fraudulent credit card transactions based on anonymized features: Using Symbolic Regression to predict rare events.
Note that the second example is a classification problem. This is not an issue: just find formulas that output 0 or 1 depending on the category.
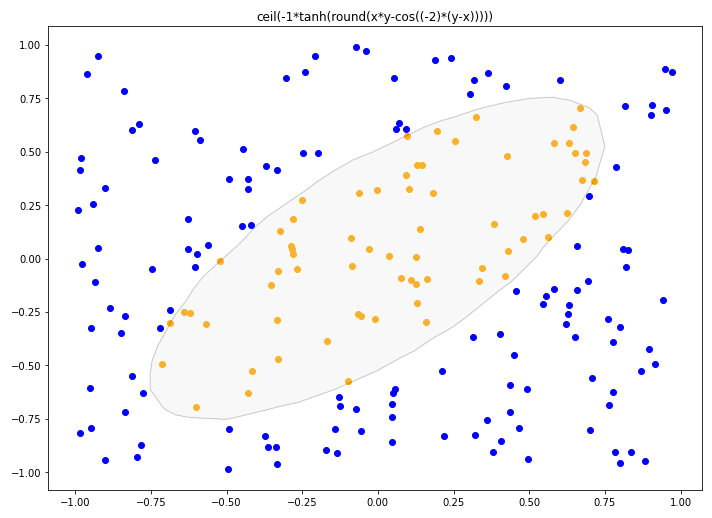
A decision boundary found with symbolic regression. Tutorial
What makes TuringBot so general is that many different search metrics are included, allowing models with different goals to be generated. Those include:
- RMS error
- Mean error
- Percentile error
- Maximum error
- Mean relative error
- Maximum relative error
- Correlation coefficient
- Hybrid (CC+RMS)
- Nash-Sutcliffe efficiency
- Residual sum of squares (RSS)
- Root mean squared log error (RMSLE)
- Classification accuracy
- F-score
- Binary cross-entropy
- Matthews correlation coefficient
Is TuringBot free?
TuringBot is free forever for datasets up to 50 rows and 3 input variables—no credit card or signup required. Just download and start discovering formulas. For larger datasets and unlimited variables, paid licenses are available on the Pricing page.
Academic publications
Used in 60+ academic publications across Engineering, Physical Sciences, and Computer Science, the program is also trusted by companies in oil & gas, manufacturing, aerospace, and more.
High-strain rate compressive behavior of fiber-reinforced rubberized concrete
Lai, D., Demartino, C., & Xiao, Y. (2022). Construction and Building Materials, 319, 125739. [URL]
Novel machine-learning-based stall delay correction model for improving blade element momentum analysis in wind turbine performance prediction
Syed Ahmed Kabir, I. F., Gajendran, M. K., Ng, E., Mehdizadeh, A., & Berrouk, A. S. (2022). Wind, 2(4), 636–658. [URL]
Finite element analysis and machine learning guided design of carbon fiber organosheet-based battery enclosures for crashworthiness
Shaikh, S. A., Taufique, M. F. N., Balusu, K., Kulkarni, S. S., Hale, F., Oleson, J., Devanathan, R., & Soulami, A. (2024). Applied Composite Materials, 31(5), 1475–1493. [URL]
Effect of the refrigerant charge, expansion restriction, and compressor speed interactions on the energy performance of household refrigerators
Knabben, F. T., Ronzoni, A. F., & Hermes, C. J. (2021). International Journal of Refrigeration, 130, 347–355. [URL]
Machine learning-based approach to wind turbine wake prediction under yawed Conditions
Gajendran, M. K., Kabir, I. F. S. A., Vadivelu, S., & Ng, E. Y. K. (2023). Journal of Marine Science and Engineering, 11(11), 2111. [URL]
Optimization and comparative evaluation of novel marine engines integrated with fuel cells using sustainable fuel choices
Seyam, S., Dincer, I., & Agelin-Chaab, M. (2024). Energy, 301, 131629. [URL]
Multi-method simulation and multi-objective optimization for energy-flexibility-potential assessment of food-production process cooling
Howard, D. A., Jørgensen, B. N., & Ma, Z. (2023). Energies, 16(3), 1514. [URL]
Yield Load Solutions for SE (B) Fracture Toughness Specimen with I-Shaped Heterogeneous Weld
Konjatić, P., Katinić, M., Kozak, D., & Gubeljak, N. (2021). Materials, 15(1), 214. [URL]
Critical review of the daylight glare probability and proposal for modification for improved evaluation of small glare sources
Geisler-Moroder, D. & Knoflach, C. (2025). Lighting Research & Technology, 14771535251314413. [URL]
An XAI framework for predicting wind turbine power under rainy conditions developed using CFD simulations
Syed Ahmed Kabir, I. F., Gajendran, M. K., Taslim, P. M. P., Boopathy, S. R., Ng, E. Y., & Mehdizadeh, A. (2024). Atmosphere, 15(8), 929. [URL]
Dynamic Economic Load Dispatch Using Linear Programming and Mathematical-Based Models.
Al-Subhi, A. (2022). Mathematical Modelling of Engineering Problems, 9(3). [URL]
Estimation of c* Integral for mismatched welded compact tension specimen
Katinić, M., Turk, D., Konjatić, P., & Kozak, D. (2021). Materials, 14(24), 7491. [URL]
Machine learning based predictive modeling of stochastic systems
Gajendran, M. K. (2023). University of Missouri-Kansas City. [URL]
Plastic Limit Pressure and Stress Intensity Factor for Cracked Elbow Containing Axial Semi-Elliptical Part-Through Crack
Damjanović, B., Konjatić, P., & Katinić, M. (2024). Applied Sciences, 14(18), 8390. [URL]
Critical comparison of different expressions for predicting the effect of loading rate on the ductile-to-brittle transition region
Wallin, K. (2025). Engineering Fracture Mechanics, 315, 110822. [URL]
Data-Driven Modeling of Power Electronic Converters Using Symbolic Regression for Digital Twin Applications
Hadifar, N., Biglo, A. H. A., Cronin, J., Wunderlich, A., Moscato, P., & Santi, E. (2025). In 2025 IEEE Electric Ship Technologies Symposium (ESTS) (pp. 135–142). [URL]
Semi-empirical equations for determining stress concentration factors in KT joints for fixed offshore platforms
de Amorim Costa, L. (2025). (Doctoral dissertation, Universidade Federal do Rio de Janeiro). [URL], in Portuguese
Experimental investigation of leakage in piston-cylinder clearance of alternative refrigeration compressors
Nicoluzzi, M. F. et al. (2022). . [URL], in Portuguese
Development of drag coefficient correlations for circular cylinder using symbolic regression
Elghannay, H. A. & El Hasadi, Y. M. (2023). Al-Mukhtar Journal of Engineering Research, 7(1), 20–28. [URL]
Materials Characterization, Prediction and Control Project: Summary Report on Data Analytics Framework
Kappagantula, K. S., Obiri, M. Y., Taufique, M. F. N., Richards, L. E., King, E., Howland, S., Bilbrey, J. A., Durell, J. L., Nguyen, J. H., Koch, J. V., et al. (2024). Pacific Northwest National Laboratory (PNNL), Richland, WA (United States). [URL]
Influence of Open Differential Design on the Mass Reduction Function
Karakašić, M., Konjatić, P., Glavaš, H., & Grgić, I. (2023). Applied Sciences, 13(24), 13300. [URL]
Buckling Resistance of Single and Double Angle Compression Members
Alenezi, A. M. M. (2022). (Doctoral dissertation, Université d'Ottawa/University of Ottawa). [URL]
Semi-empirical equation for determination of stress concentration factors (SCF) in tubular joints of fixed offshore platforms subjected to axial forces
Costa, L. A. & de Sousa, J. R. M. (2022). In XLIII Ibero-Latin American Congress on Computational Methods in Engineering (Vol. 4, No. 04). [URL]
Data-Driven Estimation of Cerchar Abrasivity Index Using Rock Geomechanical and Mineralogical Characteristics
Choi, S. & Ko, T. Y. (2026). Applied Sciences, 16(1), 552. [URL]
A Regression-Based Approach for Assessing the Buckling Coefficient of Stiffened and Unstiffened Elements
Lakshmi, J. R. & Kumar, J. V. V. (2023). In IOP Conference Series: Earth and Environmental Science (Vol. 1237, No. 1, pp. 012010). [URL]
Equations for calculating extreme tensions and curvatures at the top of flexible risers based on symbolic regression
Gomes, L. T. (2025). (Doctoral dissertation, Universidade Federal do Rio de Janeiro). [URL], in Portuguese
Data-Driven Digital Twin Based Energy Flexibility Investigation for Commercial Greenhouse Production Process
Howard, D. A., Værbak, M., Ma, Z., Jørgensen, B. N., & Ma, Z. (2024). In EPIA Conference on Artificial Intelligence (pp. 193–205). [URL]
Variable Analysis for Supporting Reservoir Impoundment Modelling
Rosita, R. H., Juwono, P. T., Limantara, L. M., & Yuliani, E. (2024). Journal of Hunan University Natural Sciences, 51(6). [URL]
A monthly-adaptive sky temperature model for the Mediterranean area based on symbolic regression: development, validation and impact on building energy simulations
Evangelisti, L., De Cristo, E., Drago, C., Battista, G., & Vollaro, R. D. L. (2025). Energy and Buildings, 116910. [URL]
Soft Magnetic Sensing on a Compliant Surface and Contact Mechanics Approximations at the Interface
Aparicio, J. (2024). . [URL]
Evaluating the suitability of linear and nonlinear regression approaches for the Langmuir adsorption model as applied toward biomass-based adsorbents: Testing residuals and assessing model validity
Mikolajczyk, A. P., Fortela, D. L. B., Berry, J. C., Chirdon, W. M., Hernandez, R. A., Gang, D. D., & Zappi, M. E. (2024). Langmuir, 40(39), 20428–20442. [URL]
From kepler to newton: Explainable AI for science discovery
Li, Z., Ji, J., & Zhang, Y. (2021). arXiv preprint arXiv:2111.12210. [URL]
Continued fractions and the Thomson problem
Moscato, P., Haque, M. N., & Moscato, A. (2023). Scientific Reports, 13(1), 7272. [URL]
The SDSS-Gaia View of the Color–Magnitude Relation for Blue Horizontal-branch Stars
Barbosa, F. O., Santucci, R. M., Rossi, S., Limberg, G., Perez-Villegas, A., & Perottoni, H. D. (2022). The Astrophysical Journal, 940(1), 30. [URL]
New alternatives to the Lennard-Jones potential
Moscato, P. & Haque, M. N. (2024). Scientific Reports, 14(1), 11169. [URL]
Effect of Water Chemistry on Polymer Retention in Carbonate Reservoirs under Harsh Conditions
Sebastian, A. (2023). PhD dissertation. [URL]
Approximating the boundaries of unstable nuclei using analytic continued fractions
Moscato, P. & Grebogi, R. (2023). In Proceedings of the Companion Conference on Genetic and Evolutionary Computation (pp. 751–754). [URL]
Approximating the nuclear binding energy using analytic continued fractions
Moscato, P. & Grebogi, R. (2024). Scientific Reports, 14(1), 11559. [URL]
Models for plasmasphere and plasmatrough density and average ion mass including dependence on L, MLT, geomagnetic activity, and phase of the solar cycle
Denton, R. E., Takahashi, K., & Hartley, D. P. (2025). Frontiers in Astronomy and Space Sciences, 11, 1459281. [URL]
A New Approximation for the Perimeter of an Ellipse
Moscato, P. & Ciezak, A. (2024). Algorithms, 17(10), 464. [URL]
The electron density at the midpoint of the plasmapause
Denton, R. E., Tengdin, P. M., Hartley, D. P., Goldstein, J., Lee, J., & Takahashi, K. (2024). Frontiers in astronomy and space sciences, 11, 1376073. [URL]
Charting New Territories: Exploring Physics Datasets through Continued Fraction Regression
Grebogi, R. B. (2024). (Doctoral dissertation, The University of Newcastle). [URL]
Galactic Archaeology through the Blue Stars of the Horizontal Branch
Barbosa, F. O. (2023). (Doctoral dissertation, Universidade de São Paulo). [URL], in Portuguese
Removal of 2, 4-Dichlorophenol From Aqueous Solutions Using Biomass Based Adsorbents: Isotherm Modeling, Performance Evaluations, and Application of Modified Cypress Sawdust
Mikolajczyk, A. P. (2024). University of Louisiana at Lafayette. [URL]
Thermophysical properties of aqueous amines solutions for CO2 capture applications
Pérez Milian, Y. et al. (2025). . [URL]
Symbolic Regression Applied to Cosmology: An Approximate Expression for the Density Perturbation Variance
Carvalho, A., Oliveira, D. M., Krone-Martins, A., & Da Silva, A. (2023). In 2023 IEEE 19th International Conference on e-Science (e-Science) (pp. 1–2). [URL]
Plasma wakes from the Baffle Scanning Mechanism on a LEO mass spectrometer
Bengtson, M., Barrie, A., & Benna, M. (2025). Physics of Plasmas, 32(4). [URL]
Logic guided genetic algorithms (student abstract)
Ashok, D., Scott, J., Wetzel, S. J., Panju, M., & Ganesh, V. (2021). In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 35, No. 18, pp. 15753–15754). [URL]
Practical level-of-detail aggregation of fur appearance
Zhu, J., Zhao, S., Wang, L., Xu, Y., & Yan, L. (2022). ACM Transactions on Graphics (TOG), 41(4), 1–17. [URL]
An analytic BRDF for materials with spherical Lambertian scatterers
d'Eon, E. (2021). In Computer Graphics Forum (Vol. 40, No. 4, pp. 153–161). [URL]
Identifying influential nodes with centrality indices combinations using symbolic regressions
Mukhtar, M. F., Abas, Z. A., Rasib, A. H. A., Anuar, S. H. H., Zaki, N. H. M., Rahman, A. F. N. A., Abidin, Z. Z., & Shibghatullah, A. S. (2022). International Journal of Advanced Computer Science and Applications, 13(5). [URL]
VMF Diffuse: A unified rough diffuse BRDF
d'Eon, E. & Weidlich, A. (2024). In Computer Graphics Forum (Vol. 43, No. 4, pp. e15149). [URL]
Global structure model modification to improve influential node detection
Mukhtar, M. F., Abas, Z., Rasib, A., Anuar, S. H. H., Zaki, N. H. M., Abidin, Z. Z., Asmai, S. A., & Rahman, A. F. N. A. (2023). Journal of Engineering and Applied Sciences, 18(3), 220–225. [URL]
Development of a physically correct light reflection model based on the calculation of the angle between vectors
Zavalniuk, Y. K., Romaniuk, O. N., Snihur, A. V., & Shevchuk, R. P. (2023). Scientific works of DonNTU, No. 2 (35), No. 1 (36): 45-50. [URL], in Ukrainian
Development of a physically correct second-degree reflection model
Zavalniuk, Y. K., Romaniuk, O. N., Pavlov, S. V., Shevchuk, R. P., & Korobeinikova, T. I. (2022). Opto-electronic information-energy technologies, 44(2), 19–25. [URL], in Ukrainian
Experimental data-efficient reinforcement learning with an ensemble of surrogate models
Jiang, J. & Chen, Z. (2025). Neural Networks, 107870. [URL]
Modification of the cosine-quadratic light reflection model for 3D image rendering
Zavalniuk, Y. K., Romaniuk, O. N., & Kotlyk, S. V. (2025). Automation of technological and business processes, 17(2): 40-49. [URL], in Ukrainian
A review of the fractal market hypothesis for trading and market price prediction
Blackledge, J. & Lamphiere, M. (2021). Mathematics, 10(1), 117. [URL]
Data-driven artificial intelligence (AI) algorithms for modelling potential maize yield under maize–legume farming systems in East Africa
Agboka, K. M., Tonnang, H. E., Abdel-Rahman, E. M., Odindi, J., Mutanga, O., & Niassy, S. (2022). Agronomy, 12(12), 3085. [URL]
New postoperative pain instrument for toddlers—Secondary analysis of prospectively collected assessments after tonsil surgery
Gude, P., Geldermann, N., Gustedt, F., Grobe, C., Weber, T., & Georgevici, A. (2024). Pediatric Anesthesia, 34(4), 347–353. [URL]
P37 Can Artificial Intelligence Methods Improve Mapping of Preference Based Measures? an Application of Symbolic Regression
Crott, R. (2023). Value in Health, 26(12), S10. [URL]
MSR223 A Comparison of of Symbolic Regression Machine Learning Methods for Mapping EQ-5D Utilities
Crott, R. (2024). Value in Health, 27(12), S482. [URL]
Optimisation of Cryptocurrency Trading Using the Fractal Market Hypothesis with Symbolic Regression
Blackledge, J. & Blackledge, A. (2025). Commodities, 4(4), 22. [URL]
Development of a Simple Method for Predicting Rice Biomass at Harvest Based on Biomass Accumulation Data
Takeuchi Eisuke, Tanaka Yu, Yoshida Hiroe, Saito Kazuki, Katsura Keisuke, & Shiraiwa Tachihiko (2022). In Proceedings of the 254th Japanese Society of Crop Science Conference (pp. 50–50). [URL], in Japanese
If you use TuringBot in your research, you can cite it as:
TuringBot Software (2020). TuringBot: Symbolic Regression Software [Computer software]. https://turingbotsoftware.com.
Community
- TuringBot Forum: a growing community where you can get help, ask questions, and connect with others who are equally interested in the software.
Documentation
Check out the detailed documentation for the software, where you can find:
The documentation provides straightforward, easy-to-follow examples that will help you get started quickly.
FAQ: How does TuringBot compare to Eureqa?
Both TuringBot and Eureqa are implementations of Symbolic Regression, but the algorithms used by each are completely different. Eureqa is based on genetic programming, while TuringBot is based on Simulated Annealing.
Eureqa was acquired by DataRobot, an enterprise machine learning platform, and is no longer commercially available.
A 2020 paper has shown that TuringBot performs noticeably better than Eureqa on a variety of Physics-inspired problems (arXiv:2010.11328). In this paper, TuringBot even managed to solve problems for which Eureqa could not find a solution at all.
Find the Formula Behind Your Data
No signup required. Free for small datasets.
 Windows
Windows
 macOS
macOS
 Linux
Linux