How to find formulas from values?

Have you ever looked at a spreadsheet full of numbers and wondered, "What's the pattern here?" Finding mathematical formulas from data isn't just satisfying—it's incredibly powerful. When you discover the formula behind your data, you unlock the ability to predict, extrapolate, and truly understand what's happening.

In this guide, I'll show you exactly how to use symbolic regression to automatically extract formulas from your data, even when it contains noise or errors. You'll see a real example using TuringBot software that takes just minutes to implement.

What exactly is symbolic regression (and why should you care)?

Unlike traditional machine learning that gives you a black-box prediction model, symbolic regression reveals the actual mathematical equation connecting your variables. Think of it as reverse-engineering the formula that generated your data.

Why does this matter? Because formulas give you:

• True understanding of relationships (not just predictions)
• The most compact way to represent your data
• The ability to extrapolate beyond your original data points
• Results you can actually explain to others

The process works by testing combinations of basic functions (like addition, multiplication, sine, exponential) to find the simplest formula that fits your data accurately. Unlike a 100-term polynomial that perfectly fits but tells you nothing useful, symbolic regression balances accuracy with simplicity—giving you insights you can actually use.

How does symbolic regression work? A real-world example

Let's walk through a practical example that shows symbolic regression in action. We'll create some noisy data and see if we can discover the original formula.

Step 1: Creating test data (that we'll pretend we don't understand)

First, let's generate some data based on the formula x*cos(10*x) + 2 and add random noise to simulate real-world measurement errors:

import numpy as np
import matplotlib.pyplot as plt

# Generate data: x values from 0 to 1, y values from cosine function with noise
x = np.linspace(0, 1, 100)
y = np.cos(10 * x) * x + 2 + np.random.random(len(x)) * 0.1

# Save x and y columns to a text file
np.savetxt('input.txt', np.column_stack((x, y)), fmt='%f')

# Create a plot
plt.figure(figsize=(5.5, 4))
plt.plot(x, y, color='blue')
plt.title('Cosine Function with Noise')
plt.xlabel('X values')
plt.ylabel('Y values')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('data_plot.png')
plt.show()

Here's what our mystery data looks like:

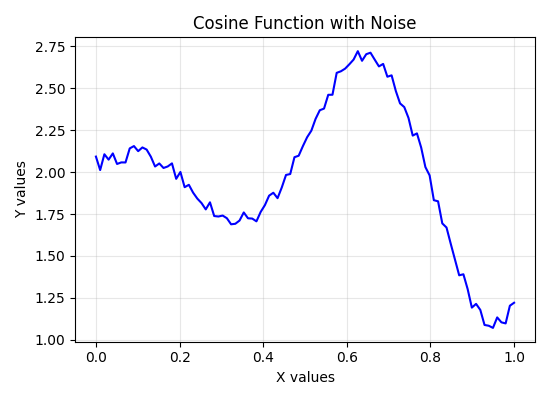
Can you tell what formula created this pattern? Not easy, right? That wavy pattern with random fluctuations could come from countless possible equations.

Step 2: Discovering the hidden formula with TuringBot

Now for the exciting part. We'll feed this data into TuringBot and see if it can uncover the original formula hidden beneath the noise:

1. Save your data as a simple text file (x values in first column, y values in second)
2. Import into TuringBot with a few clicks
3. Start the search process
4. Watch as it explores thousands of possible formulas

After just about a minute of computation, TuringBot presents its discoveries:

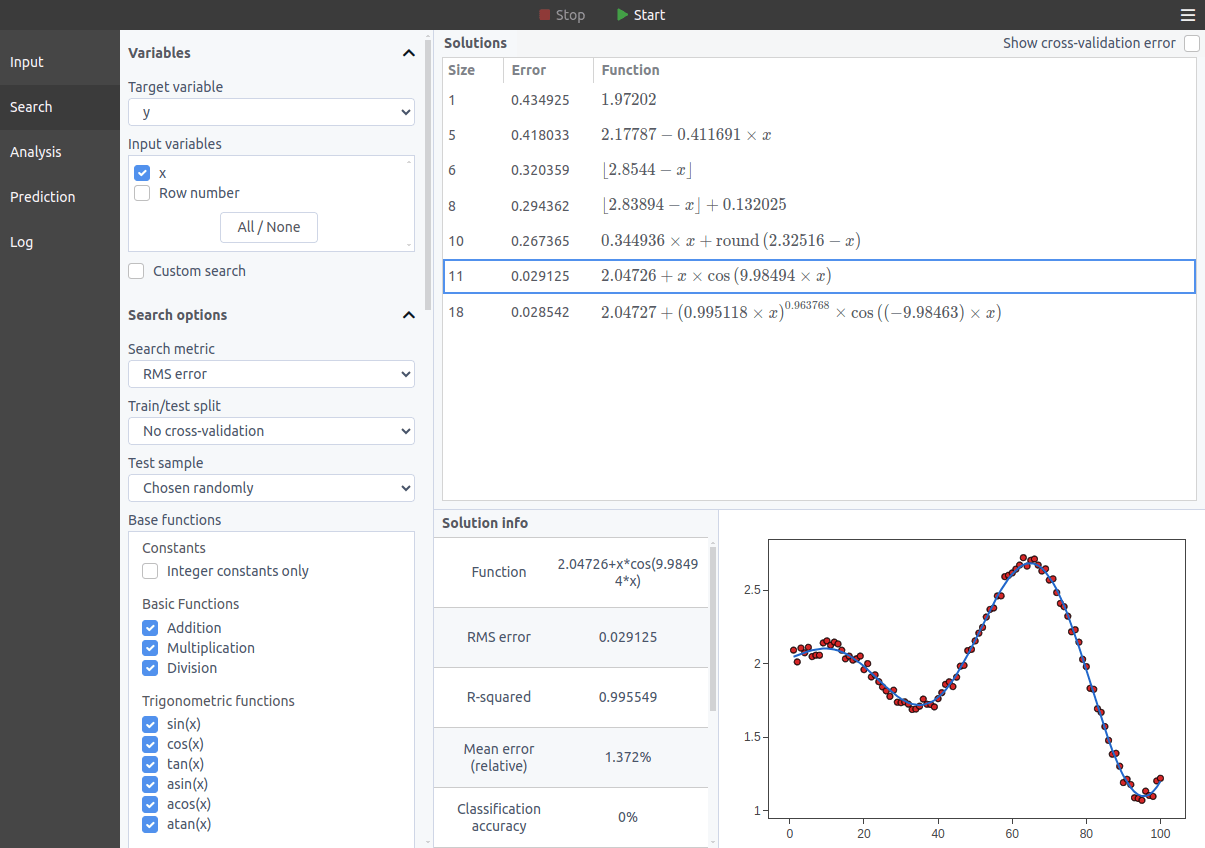
Amazing! TuringBot successfully recovered our original formula x*cos(10*x)+2 despite all the random noise we added! It also found simpler approximations that might be good enough depending on your needs.

When should you use symbolic regression instead of other techniques?

Symbolic regression shines when:

• You need to understand why something happens, not just predict what will happen
• You're working in science or engineering where interpretable models matter
• You need to deploy your model in memory-constrained environments
• You need to extrapolate far beyond your training data
• You need to communicate your findings with clear mathematical expressions

While neural networks might give slightly more accurate predictions in some cases, they can't match the clarity and insight of an actual formula.

Can symbolic regression handle complex real-world problems?

Absolutely! Our example used just one input variable, but symbolic regression works just as well with:

• Multiple input variables (like predicting temperature based on pressure, volume, and time)
• Complex interactions (discovering which variables actually matter)
• Real-world noise and outliers (as we demonstrated)

Scientists have used this technique to rediscover physical laws from experimental data. Engineers use it to create simplified models of complex systems. Researchers apply it to uncover patterns in various domains from physics to biology.

How to start finding formulas in your own data today

Ready to discover the formulas hiding in your own data? Here's how to get started:

1. Download TuringBot from the official website (the free version lets you try the core features)
2. Prepare your dataset as a simple text file with columns for each variable
3. Import your data and let TuringBot start searching for patterns
4. Experiment with different settings to control complexity vs. accuracy

The process is surprisingly straightforward—you can go from raw data to mathematical formulas in minutes.

Unlock the mathematical secrets in your data

Finding formulas from values represents a different approach to data analysis—one that prioritizes understanding over mere prediction. When you discover the mathematical relationships driving your data, you gain insights that no black-box model can provide.

Whether you're analyzing scientific measurements, engineering parameters, or experimental results, symbolic regression offers a powerful way to see the mathematical patterns that lie beneath the surface.

Try TuringBot today and transform your confusing columns of numbers into clear, insightful mathematical formulas. Your data is trying to tell you something—symbolic regression helps you understand exactly what it's saying.