- Detected credit card fraud with 87% precision and 80% recall (F1 = 0.83)
- Dataset: 284,807 transactions, only 492 frauds (0.17% positive rate)
- Output is an explicit formula—fully auditable for regulatory compliance
- TuringBot's F1 score metric handles imbalanced datasets automatically
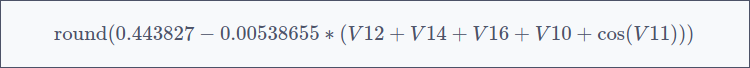
Fraud Detection: Symbolic Regression vs. Black-Box Models
| Aspect | TuringBot Formula | Neural Network / XGBoost |
|---|---|---|
| Audit trail | Full (explicit formula) | Black box—requires explainability tools |
| Regulatory compliance | Formula can be documented | Challenging to explain decisions |
| Deployment | Single equation—any language | Requires ML frameworks |
| Feature insight | Visible in formula | SHAP values needed |
Dataset: Kaggle Credit Card Fraud
Source: Kaggle Credit Card Fraud Detection (284,807 transactions, 492 frauds = 0.17%)
Symbolic regression
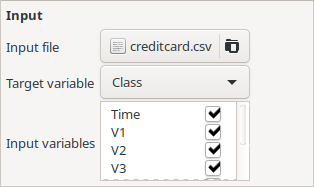
Generating symbolic models using TuringBot is a straightforward process, which requires no data science skills. The first step is to open the program and load the input file by clicking on the “Input” button, shown below. After loading, the code will automatically define the column “Class” as the target variable and all other ones as input variables, which is what we want.
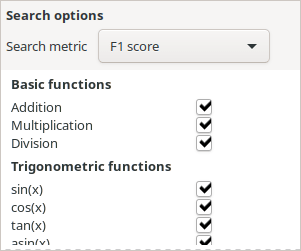
Then, we select the error metric for the search as “F1 score”, which is the appropriate one for binary classification problems on highly imbalanced datasets like this one. This metric corresponds to a geometric mean of precision and the recall of the model. A very illustrative image that explains what precision and recall are can be found on the Wikipedia page for the F1 score.
That’s it! After those two steps, the search is ready to start. Just click on the “play” button at the top of the interface. The best solutions that the program has encountered so far will be shown in the “Solutions” box in real time.
Bear in mind that this is a relatively large dataset and that it may seem like not much is going on in the first minutes of the optimization. Ideally, you should leave the program running until at least a few million formulas have been tested (you can see the number so far in the Log tab). In a modest i7-3770 CPU with 8 threads, this took us about 6 hours. A more powerful CPU would take less time.
The resulting formula
The models that were encountered by the program after this time were the following:
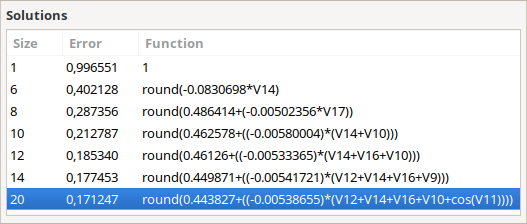
The error for the best one is 0.17, meaning its F1 score is 1 – 0.17 = 0.83. This implies that both the recall and the precision of the model are close to 83%. In a verification using Python, we have found that they are 80% and 87% respectively.
Results: 87% Precision, 80% Recall
The discovered formula:
- Detects 80% of all frauds (recall)
- Is correct 87% of the time when flagging fraud (precision)
- F1 score: 0.83—competitive with state-of-the-art ML models
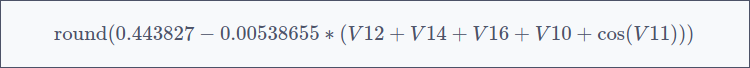
Why Formulas Matter for Fraud Detection
- Regulatory audits: Show exactly how decisions are made
- Real-time scoring: Formula computes in microseconds
- No ML infrastructure: Deploy in SQL, Java, or any language
Download TuringBot to build interpretable fraud detection models on your own datasets.