By Giovanni Di Maria, creator of EDM Electronics Design Master

A Chess Engine is a computer program that receives a move as input and returns a counter move as an answer. Here we will not delve into the theory that underlies the functioning of Chess Engines, but we will focus our attention on the representation of the chessboard relative to the initial position of a game, deepening a mathematical method to get there, using the TuringBot program.
The starting position
For those who are familiar with the game of chess, they know that the pieces are placed on the board in a very particular way, as evidenced by the figure below.

From left to right there are:
- rook;
- the knight;
- the bishop;
- Queen;
- the king;
- the bishop;
- the knight;
- rook.
The black pieces are arranged similarly: the Queens are on the squares of their color: the white Queen on the white square and the black Queen on the black square.
How to represent the chessboard in memory
There are many methods for representing a chessboard in memory. We focus our attention on reproducing the starting position using an 8×8 matrix. The basic idea is this, then the programmer can vary the method according to his needs. This in-memory representation is necessary because the program must know the game situation, especially at the start of the game. A possible solution, extremely clear and simple, perhaps banal, consists in memorizing the initials of the chess pieces in the matrix, distinguishing them between white and black with upper and lower case. This solution immediately provides a clear reading of the source code.
void reset_chessboard()
{
int x, y;
// -------Empty chessboard---------
for (x = 1; x <= 8; x++)
for (y = 1; y <= 8; y++)
chessboard[x][y] = '-';
// ----Pawns-------
for (x = 1; x <= 8; x++)
{
chessboard[x][2] = 'P';
chessboard[x][7] = 'p';
}
// ------knight------
chessboard[2][1] = 'N';
chessboard[7][1] = 'N';
chessboard[2][8] = 'n';
chessboard[7][8] = 'n';
// ------Bishop--------
chessboard[3][1] = 'B';
chessboard[6][1] = 'B';
chessboard[3][8] = 'b';
chessboard[6][8] = 'b';
// ----Rook---------
chessboard[1][1] = 'R';
chessboard[8][1] = 'R';
chessboard[1][8] = 'r';
chessboard[8][8] = 'r';
// -----Queen-----
chessboard[4][1] = 'Q';
chessboard[4][8] = 'q';
// -----King-------
chessboard[5][1] = 'K';
chessboard[5][8] = 'k';
return;
}
The mathematical approach with TuringBot
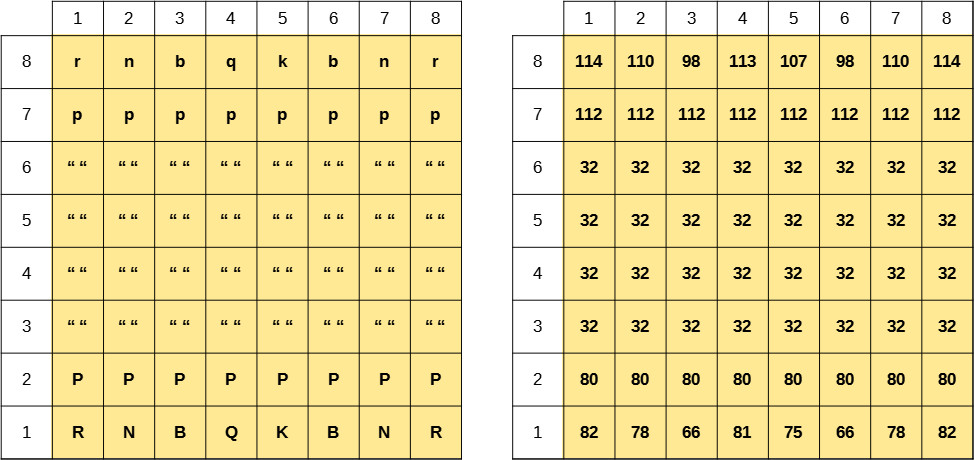
A very elegant solution is to perform the processing and storage of the initial characters of the pieces through two simple nested cycles, within which a formula, found by TuringBot, calculates the ASCII code to be inserted in each cell of the matrix. The basic idea follows the diagrams illustrated below.
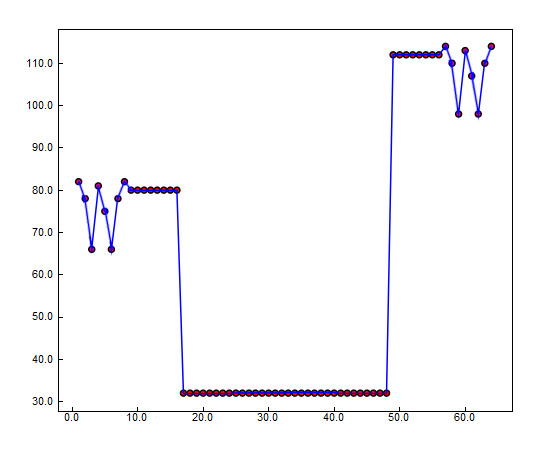
As can be seen in the matrix on the right (completely equivalent to the one on the left), in each element of the square matrix there is an ASCII numeric code that corresponds to the character that distinguishes each piece. The empty box is represented by a space (ASCII code 32). Recall that each box of a matrix is identified by two values, one of row and one of column. These values can be saved in a text file, consisting of 64 lines and 3 columns. It will be the TuringBot Input file.
1 1 82
1 2 78
1 3 66
1 4 81
1 5 75
1 6 66
1 7 78
1 8 82
2 1 80
2 2 80
2 3 80
2 4 80
2 5 80
2 6 80
2 7 80
2 8 80
3 1 32
3 2 32
3 3 32
3 4 32
3 5 32
3 6 32
3 7 32
3 8 32
4 1 32
4 2 32
4 3 32
4 4 32
4 5 32
4 6 32
4 7 32
4 8 32
5 1 32
5 2 32
5 3 32
5 4 32
5 5 32
5 6 32
5 7 32
5 8 32
6 1 32
6 2 32
6 3 32
6 4 32
6 5 32
6 6 32
6 7 32
6 8 32
7 1 112
7 2 112
7 3 112
7 4 112
7 5 112
7 6 112
7 7 112
7 8 112
8 1 114
8 2 110
8 3 98
8 4 113
8 5 107
8 6 98
8 7 110
8 8 114
Processing and research with TuringBot
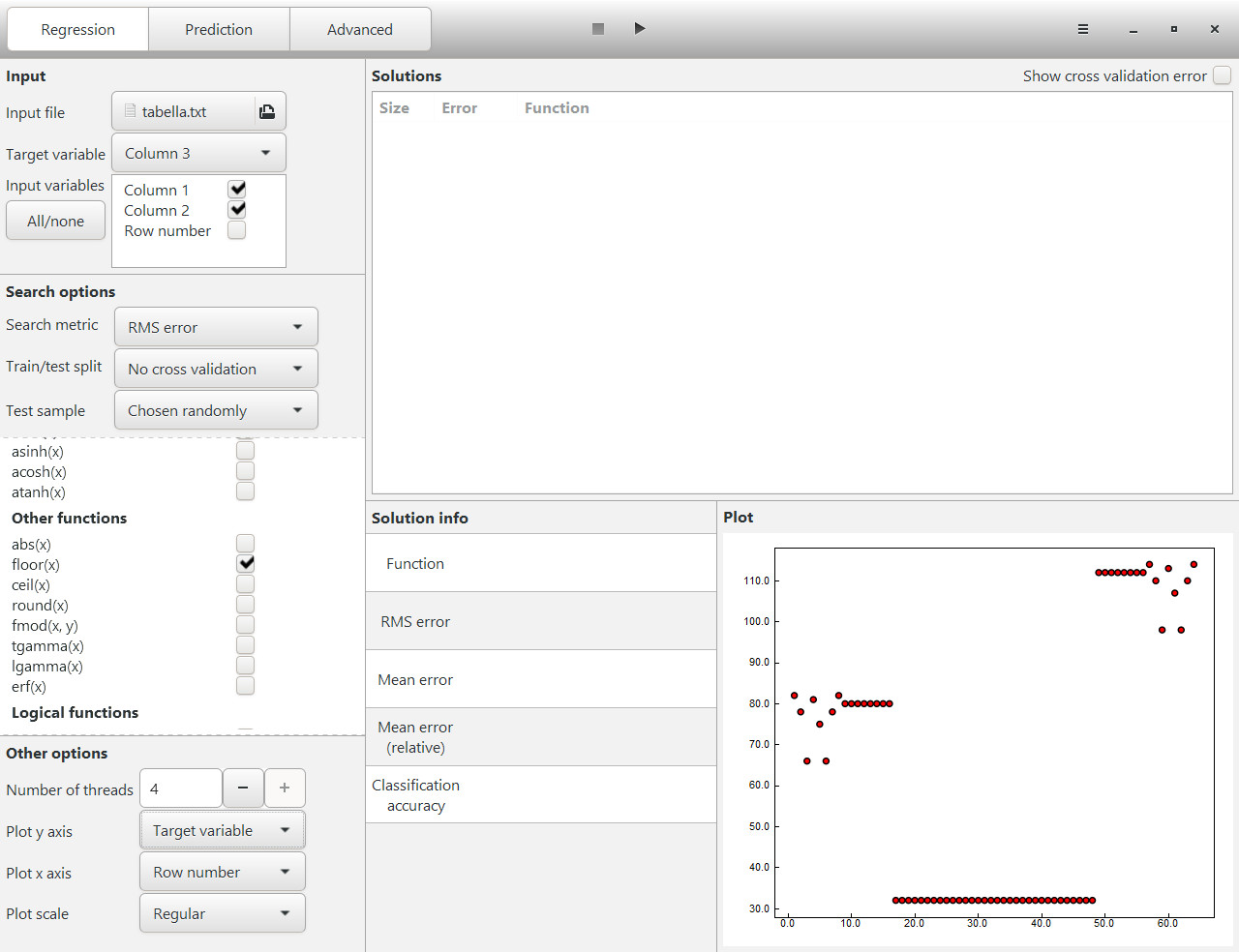
After opening the input file in TuringBot, you can configure some search parameters to better optimize this operation. Some functions are not necessary. In our case, the following search parameters have been entered:
-
Basic functions
Addition
- Multiplication
- Division
Trigonometric functions
- cos (x)
Other functions
- floor (x)
Of course, you can try other functions. The search procedure is quite long as the final formula is very complex. The screenshot below shows some initial setup steps. After setting the values, you can start the search by pressing the appropriate button.
The research begins and the program begins to generate many formulas, with a solution ever closer to the final goal. A continuously updated window shows the formulas found, in order of length and error. Normally the longer formulas provide the best results.
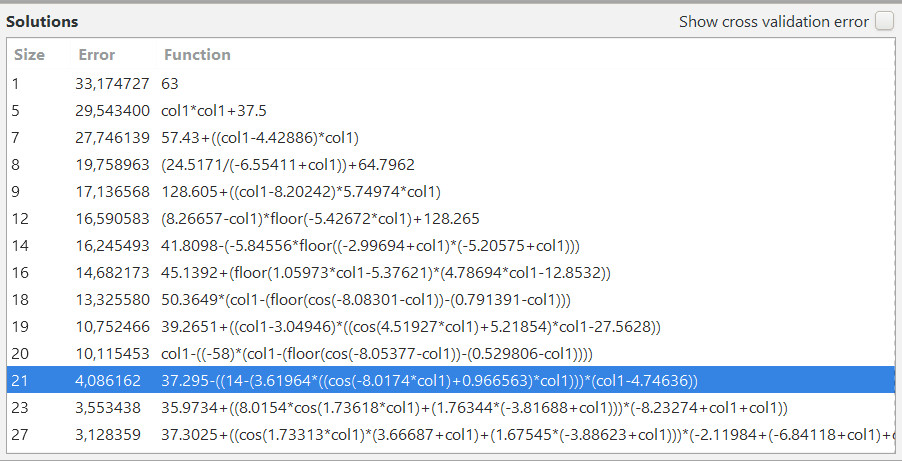
Each formula is also characterized, of course, by a graph that should follow the trend of the original data. A perfect formula always lies above all input points.
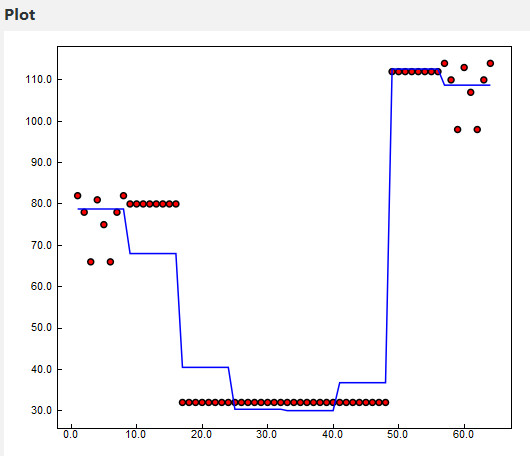
Final results
The search field is extremely vast and the final result is not always perfect, with a difference of zero. In this case, luck wanted the system to find an excellent formula that perfectly described the initial arrangement of the pieces on the board. The search took about 4 hours, using 4 Threads. This timing depends on the computer used and the number of processes used for the operation. Below are the different formulas found by TuringBot:
| Complexity | Error | Function |
|---|---|---|
| 1 | 33.1747 | 63 |
| 5 | 29.5434 | 37.5+col1*col1 |
| 7 | 27.7461 | col1*(-4.42857+col1)+57.4285 |
| 8 | 18.4378 | 37.8919*sin(col1)+55.6912 |
| 9 | 17.1364 | 128.854-(-5.76178*col1*(col1-8.20656)) |
| 10 | 15.3544 | 7.64726*col1*sin(col1)+57.17 |
| 12 | 13.7837 | 31.3877+(5.355*(7.2754*sin(col1)+col1)) |
| 13 | 11.8137 | 32+(62*greater(sin(col1),0.555342)) |
| 14 | 10.6011 | 7.09756*abs(col1+10.0746*sin(col1)) |
| 15 | 7.121 | (13.9153/cos(floor(0.732407*col1)))+58.555 |
| 17 | 3.87582 | 32+(greater(sin(col1),0.415717)*(5.18918*col1+38.6487)) |
| 18 | 3.5793 | abs(30.9689-(-6.10071*sin(1.05488*col1)*(7.47296+col1))) |
| 20 | 3.11301 | 31.4802+pow(11.7402*(col1+5.71344),cos(1.04974*col1-1.56687)) |
| 27 | 3.02812 | 31.4787+pow((11.6058+(0.68396/(col2*col2)))*(col1+5.71681),cos(1.04968*col1-1.56654)) |
| 28 | 2.48017 | 31.4839+pow((11.6357-cos(4.18524*col2))*(col1+5.69307),cos(1.04935*col1-1.56473)) |
| 30 | 2.42225 | 31.4835+pow((11.6154-cos(4.26395*(-0.110504+col2)))*(col1+5.69428),cos(1.04932*col1-1.56459)) |
| 33 | 2.35706 | 32-((38.2449+((cos(col1)+4.90525)*(col1-cos((-2.01944)*(0.23205+col2)))))*floor(cos(-58.3057-col1))) |
| 35 | 2.2992 | 32.0001-((38.2972+((1.28923*cos(col1)+4.83299)*(col1-cos(2.02027*(0.230258+col2)))))*floor(cos(-58.3057-col1))) |
| 38 | 2.02593 | 32.0005-(floor(cos(col1+1.83754))*(5.12705*(8.04121-((0.818858-cos(-34.9995*col1))*(cos(2.09691*col2)+0.6415))+col1))) |
| 40 | 1.75589 | 32.0028-(floor(cos(col1+1.78588))*(5.18838*(8.15112-((0.78022-cos(34.8496*col1+0.883278))*(cos(2.09681*col2)+0.945564))+col1))) |
| 41 | 1.52332 | 32-(floor(cos(col1+1.78119))*(4.96845*(8.04125-floor((0.939273-cos(34.9916*col1))*(cos(-2.0859*col2)+0.624216))+col1))) |
| 43 | 1.11312 | 32-(floor(cos(col1+1.8017))*(5.12004*(cos(col1)+7.83221-((0.78464-cos(-34.9183*col1))*(cos(2.09684*col2)+0.591668))+col1))) |
| 45 | 0.760652 | 32.0002-(floor(cos(col1+1.73726))*(5.12047*(cos(col1)+7.831-((0.783564-cos(34.9177*col1))*(cos((-2.00884)*(col2+0.259462))+0.612137))+col1))) |
| 48 | 0.728869 | floor(32-(floor(cos(col1+1.73299))*(5.12841*(col1+7.95556-((0.779654-cos(34.9151*col1))*(cos(1.97953*(col2+0.346471))+0.636367))+cos(col1))))) |
| 53 | 0.413448 | 32.0002-(floor(cos(col1+1.81624))*(5.11899*(col1+7.82369-((0.754511-cos(-34.913*col1))*(cos((-2.01269)*(col2+(0.0352432/cos(col2))+0.268925))+0.648806))+cos(col1)))) |
| 55 | 0.12666 | 32.0005-(floor(cos(col1+1.78631))*(5.12029*(cos(col1)+7.8269-((0.771208-cos(34.9154*col1))*(cos((-1.98154)*(col2+0.178865*cos(-5.37724+col2)+0.351792))+0.63671))+col1))) |
| 57 | 0.0580828 | 32-(floor(cos(col1+1.81682))*(5.11347*(col1+7.83564-((0.769821-cos(-34.9072*col1))*(cos((-1.98027)*(col2+0.180734*cos(-5.38204+col2)+0.35485))+0.644024))+1.07536*cos(col1)))) |
| 58 | 0 | floor(32-(floor(cos(col1+1.73299))*(5.12816*(col1+7.89449-((0.770326-cos(34.9151*col1))*(cos(1.97953*(col2+0.181536*cos(-5.37362+col2)+0.35012))+0.636367))+cos(col1))))) |
The final formula, therefore, which perfectly calculates the ASCII code of the piece on a box, given an “x” and “y” position, is the following:
floor(32-(floor(cos(x+1.73299))*(5.12816*(x+7.89449-((0.770326-cos(34.9151*x))*(cos(1.97953*(y+0.181536*cos(-5.37362+y)+0.35012))+0.636367))+cos(x)))))
The formula can be implemented in all programming languages. The following example was created for the PARI / GP program:
{
for(x=1,8,
for(y=1,8,
z=floor(32-(floor(cos(x+1.73299))*(5.12816*(x+7.89449-((0.770326-cos(34.9151*x))*(cos(1.97953*(y+0.181536*cos(-5.37362+y)+0.35012))+0.636367))+cos(x))))) ;
print(x," ",y," ",z);
);
);
}
The execution of the simple listing, which contemplates the long but powerful mathematical formula, generates the following list of values, perfectly corresponding with the previous one.
1 1 82
1 2 78
1 3 66
1 4 81
1 5 75
1 6 66
1 7 78
1 8 82
2 1 80
2 2 80
2 3 80
2 4 80
2 5 80
2 6 80
2 7 80
2 8 80
3 1 32
3 2 32
3 3 32
3 4 32
3 5 32
3 6 32
3 7 32
3 8 32
4 1 32
4 2 32
4 3 32
4 4 32
4 5 32
4 6 32
4 7 32
4 8 32
5 1 32
5 2 32
5 3 32
5 4 32
5 5 32
5 6 32
5 7 32
5 8 32
6 1 32
6 2 32
6 3 32
6 4 32
6 5 32
6 6 32
6 7 32
6 8 32
7 1 112
7 2 112
7 3 112
7 4 112
7 5 112
7 6 112
7 7 112
7 8 112
8 1 114
8 2 110
8 3 98
8 4 113
8 5 107
8 6 98
8 7 110
8 8 114
When the curve fits perfectly to the points of the input data, with zero error, it means that the final formula has been found!