Symbolic regression is a machine learning technique capable of generating models that are explicit and easy to understand.
In this tutorial, we are going to generate our first symbolic regression model. For that, we are going to use the TuringBot software. After generating the model, we are going to visualize the results using a Python library (Matplotlib).
To make things more interesting, we are going to try to find a mathematical formula for the N-th prime number (A000040 in the OEIS).
Symbolic regression setup
The symbolic regression software that we are going to use is called TuringBot. It is a desktop application that runs on both Windows and Linux. The usage is straightforward: you load your input file in .txt or .csv format, select which column should be predicted and which columns should be used as input, and then start the search.
Several search metrics are available, including RMS error, mean error, correlation coefficient, and others. Since we are interested in predicting the exact values of the prime numbers, we are going to use the “classification accuracy” metric.
This is what the interface looks like after loading the input file containing prime numbers as a function of N, which we have truncated to the first 20 rows:
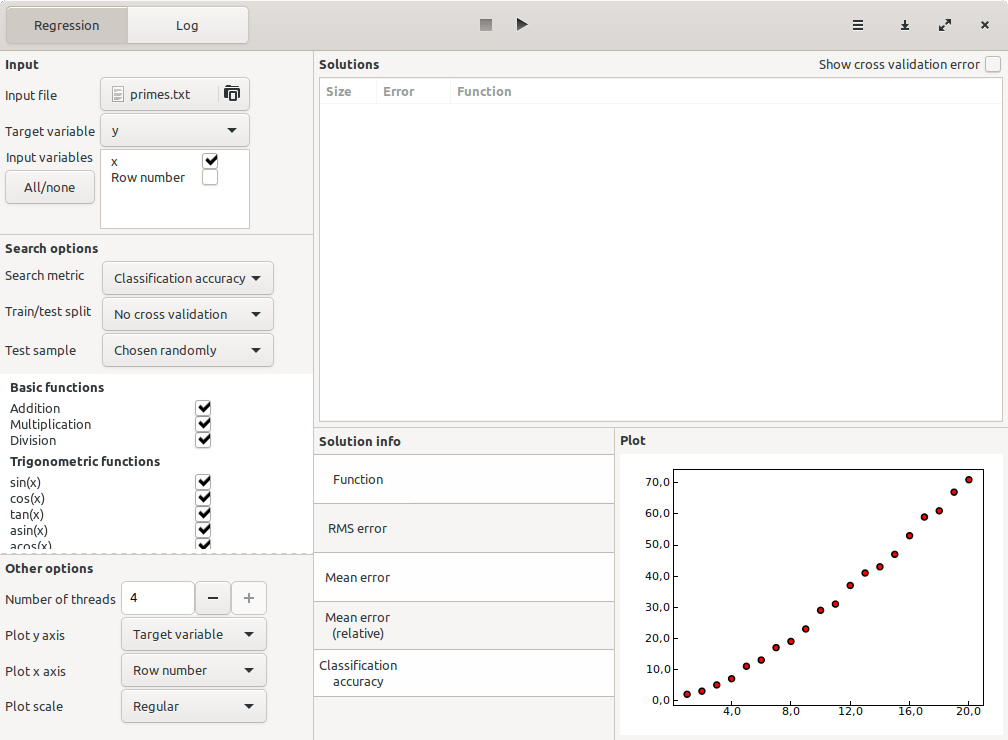
With the input file loaded and the search metric selected, the search can be started by clicking on the play button at the top of the interface.
The formulas that were found
After letting TuringBot work for a few minutes, these were the formulas that it ended up finding:
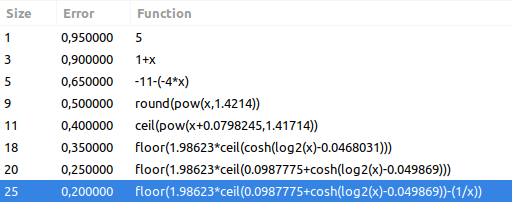
The best one has an error of 0.20, that is, a classification accuracy of 80%. Which is quite impressive considering how short the formula is. Of course, we could have obtained a 100% accuracy with a huge polynomial, but that would not compress the data in any way, since the number of free parameters in the resulting model would be the same as the number of data points.
Visualizing with Python
Now we can finally visualize the symbolic model using Python. Luckily the formula works out of the box as long as we import the math library (TuringBot follows the same naming convention). This is what the script looks like:
import numpy as np
import matplotlib.pyplot as plt
from math import floor, ceil, cosh, log2
def prime(x):
return floor(1.98623 * ceil(0.0987775 + cosh(log2(x) - 0.049869)) - (1 / x))
# Load data from 'primes.txt'
data = np.loadtxt('primes.txt')
# Scatter plot of the data
plt.scatter(data[:, 0], data[:, 1], label='Data')
# Plot the model based on the prime function
plt.plot(data[:, 0], [prime(x) for x in data[:, 0]], label='Model')
# Add labels and title
plt.xlabel('N')
plt.ylabel('Prime Values')
plt.title('Prime Numbers')
plt.legend()
# Show the plot
plt.show()
And this is the resulting plot:
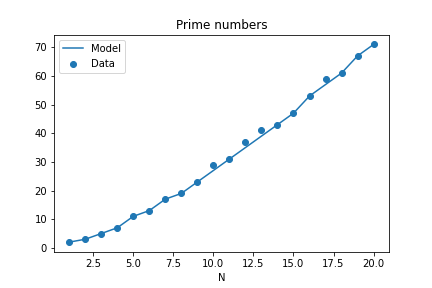
Conclusion
In this tutorial, we have seen how to generate a symbolic regression model. The example given was a very simple one, with only one input variable and a small number of data points, but the methodology would work just as fine with a real-world large dataset with multiple dimensions, allowing a variety of machine learning problems of practical interest to be solved.